[Swift] Leetcode 684. Redundant Connection

684. Redundant Connection

 

In this problem, a tree is an undirected graph that is connected and has no cycles.

 

The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, ..., N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.

 

The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.

 

Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.

 

Example 1

 Input: [[1,2], [1,3], [2,3]]

 Output: [2,3]

 Explanation: The given undirected graph will be like this:

   1

  / \

 2 - 3

 

Example 2

  Input: [[1,2], [2,3], [3,4], [1,4], [1,5]]

  Output: [1,4]

  Explanation: The given undirected graph will be like this:

  5 - 1 - 2

      |   |

      4 - 3

 

 Note:

 The size of the input 2D-array will be between 3 and 1000.

 Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.

 

Coding!

Detect Cycle in an Undirected Graph Set 1

 

전체코드는 684-1, 684-2에서 확인할 수 있습니다.

 

 DSU (Disjoint Set Union) 두 가지 메소드를 가지고 있습니다.

• find(node:): 두 요소가 동일한 하위 집합에 있는지 확인하는 데 사용할 수 있습니다. (부모가 같은지 찾음)
• union(node:, node:): 두 개의 하위 집합을 단일 하위 집합으로 결합 (부모가 같다면 같은 부모로 연결합니다.)

extension Array where Element == Int {
    func findParent(parent: inout [Int], node: Int) -> Int {
        if parent[node] == -1 {
            return node
        }
        return findParent(parent: &parent, node: parent[node])
    }
    func union(parent: inout [Int], x: Int, y: Int) {
        let xset = findParent(parent: &parent, node: x)
        let yset = findParent(parent: &parent, node: y)
        parent[xset] = yset
    }
}

class Solution {
    func findRedundantConnection(_ edges: [[Int]]) -> [Int] {
        return findCyclic(edges)
    }

    func findCyclic(_ edges: [[Int]]) -> [Int] {
        // Allocate memory for creating subsets
        // Initialize all subsets as single element sets
        var parent = Array(repeating: -1, count: edges.count + 1)

        for (i, edge) in edges.enumerated() {
            let x = edge.findParent(parent: &parent, node: edge[0])
            let y = edge.findParent(parent: &parent, node: edge[1])
            if x == y {
                return edge
            }

            edge.union(parent: &parent, x: x, y: y)
        }
        return [-1, -1]
    }
}

우리는 그래프가 순환하는지 찾아내야합니다.

 

1. Parent 서브셋을 생성하고 -1로 초기화 합니다.

1회전 (0, 1)

 

2회전 (1, 2)

 

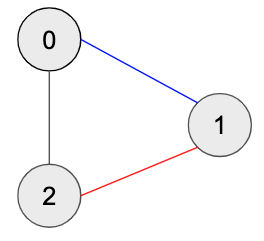
3회전 (0, 2)

부모가 만약 -1 이었다면 Cycle 이 아니였을 것입니다. 

그러나 X, Y 축이 부모가 모두 2를 가르키고 있기 때문에 Cycle 이 있다고 판단합니다. 

 

 

Complexity analysis

Time complexity: ??? O(N) 잘모르겠음 

Space complexity: O(N)

 

Running

Runtime: 32ms

Memory: 21MB

 

Log

====== 0 ======= 
edge: [0, 1]
x: [-1, -1, -1]
y: [-1, -1, -1]
x: 0, y: 1
union(parent:x:y:) xset: 0, yset: 1
after union: [1, -1, -1]

====== 1 ======= 
edge: [1, 2]
x: [1, -1, -1]
y: [1, -1, -1]
x: 1, y: 2
union(parent:x:y:) xset: 1, yset: 2
after union: [1, 2, -1]

====== 2 ======= 
edge: [0, 2]
findParent(parent:node:) found parent: 2
findParent(parent:node:) found parent: 2
x: [1, 2, -1]
y: [1, 2, -1]
x: 2, y: 2

 

Detect Cycle in an Undirected Graph Set 2

(Union By Rank and Path Compression)

 

전체코드는 684-1, 684-2에서 확인할 수 있습니다.

 

union() find() 의 최악 시간복잡도는 Linear O(N) 이 됩니다.

아래 그림은 최악 시나리오 예입니다.

 

 

 

 

Union by rank

O(N) -> O(Log n) 으로 최적화 시킬 수 있습니다. 

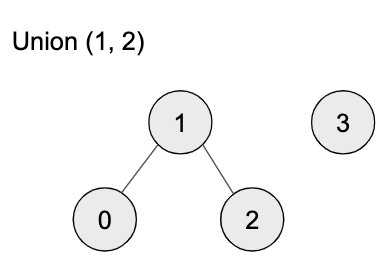
Path Compression

Find()가 호출 될 때 트리를 Flattern 하도록 만듭니다. 

 

Find(3) 을 호출하면 3을 9의 자식으로 만듭니다.

 

struct Subset {
    var parent: Int
    var rank: Int
}

extension Array where Element == Int {
    func findParent(subsets: inout [Subset], i: Int) -> Int {
        if subsets[i].parent != i {
            // Path compression
            subsets[i].parent = findParent(subsets: &subsets, i: subsets[i].parent)
        }
        return subsets[i].parent
    }
    func union(subsets: inout [Subset], x: Int, y: Int) {
        let xroot = findParent(subsets: &subsets, i: x)
        let yroot = findParent(subsets: &subsets, i: y)

        // union-by-rank
        if subsets[xroot].rank < subsets[yroot].rank {
            subsets[xroot].parent = yroot
        } else if subsets[xroot].rank > subsets[yroot].rank {
            subsets[yroot].parent = xroot
        } else {
            subsets[yroot].parent = xroot
            subsets[xroot].rank += 1
        }
    }
}

class Solution {
    func findRedundantConnection(_ edges: [[Int]]) -> [Int] {
        return findCyclic(edges)
    }

    func findCyclic(_ edges: [[Int]]) -> [Int] {
        var subsets: [Subset] = []
        (0...edges.count).forEach {
            subsets.append(Subset(parent: $0, rank: 0))
        }

        for (i, edge) in edges.enumerated() {
            let x = edge.findParent(subsets: &subsets, i: edge[0])
            let y = edge.findParent(subsets: &subsets, i: edge[1])

            if x == y {
                return edge
            }

            edge.union(subsets: &subsets, x: x, y: y)

        }
        return [-1, -1]
    }
}

Complexity analysis

Time complexity: O(N)

Space complexity: O(N)

 

Running

Runtime: 48ms

Memory: 21.2MB

 

마무리

전체코드는 684-1, 684-2에서 확인할 수 있습니다.