[Swift] Leetcode 209. Minimum Size Subarray Sum

209. Minimum Size Subarray Sum

 

Given an array of n positive integers and a positive integer s, find the minimal length of a contiguous subarray of which the sum ≥ s. If there isn't one, return 0 instead.

 

Example: 

Input: s = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: the subarray [4,3] has the minimal length under the problem constraint.

 

 

Coding!

Using Binary search

 func minSubArrayLen(_ s: Int, _ nums: [Int]) -> Int {
        if nums.count == 0 {
            return 0
        }
        
        var sums = [Int](repeatElement(0, count: nums.count + 1))
        var result = Int.max
        
        for i in 1..<sums.count {
            sums[i] = sums[i - 1] + nums[i - 1]
        }
        for i in 0..<sums.count {

            let end = binarySearch(i + 1, sums.count - 1, sums, sums[i] + s)
            if end == sums.count {
                break
            }
            if end - i < result {
                result = end - i
                print("\(result) = \(end) - \(i)")
            }
        }
        
        return result == Int.max ? 0 : result
    }
    private func binarySearch(_ left: Int, _ right:Int, _ nums: [Int], _ target: Int) -> Int {
        var left = left
        var right = right
        var middle = 0
        
        while left <= right {
            middle = (left + right) / 2
            if nums[middle] < target {
                left = middle + 1
            } else {
                right = middle - 1
            }
        }
        return left
    }

 

Complexity analysis

• Time complexity: O(n log(n))
• Space complexity: O(1)

 

1. Array Size + 1 크기로 0으로 초기화

2. 이전 값을 누적해서 값을 저장합니다.

 

 

3. (1회전) binarySearch(left: 1, right: 6, nums: [0, 2, 5, 6, 8, 12, 15], target: 0 + 7)

4. (2회전) binarySearch(left: 2, right: 6, nums: [0, 2, 5, 6, 8, 12, 15], target: 2 + 7)

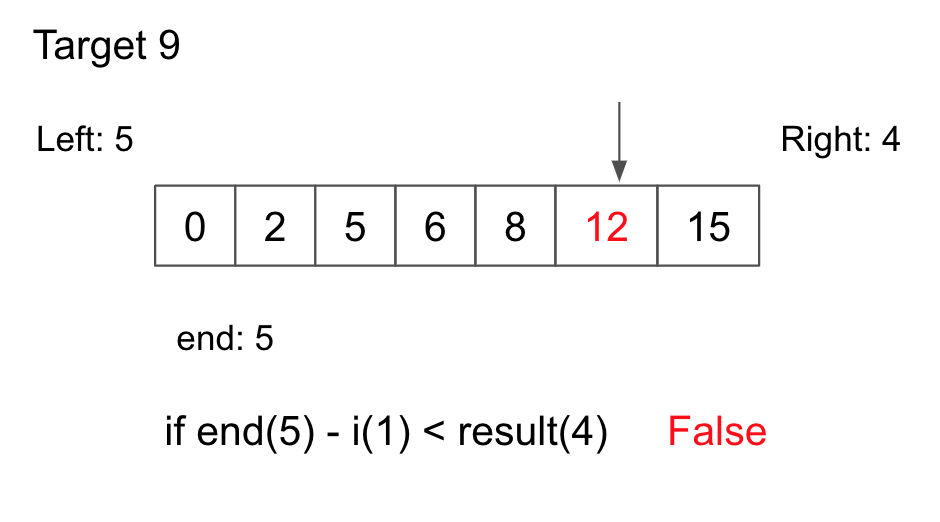
5. (3회전) binarySearch(left: 3, right: 6, nums: [0, 2, 5, 6, 8, 12, 15], target: 5 + 7)

 

 

6. (4회전) binarySearch(left: 4, right: 6, nums: [0, 2, 5, 6, 8, 12, 15], target: 6 + 7)

 

 

 

7. (4회전) binarySearch(left: 5, right: 6, nums: [0, 2, 5, 6, 8, 12, 15], target: 8 + 7)

 

 

가장 마지막이 최소값이므로 Result(2) 답이다.

 

Using 2 pointers

지금까지는 SubArray의 시작 인덱스를 고정하여 마지막 위치를 찾았습니다.

우리는 현재 SubArray의 시작과 끝을 위한 2 개의 포인터를 유지할 수 있습니다. 

 

 func minSubArrayLen(_ s: Int, _ nums: [Int]) -> Int {
        let size = nums.count
        var ans = Int.max
        var left = 0
        var sum = 0
        
        for i in (0..<size) {
            sum += nums[i]
            print("i: { \(i) } \(sum) >= \(s) ")
            while sum >= s {
                let preAns = ans
                let result = i + 1 - left
                ans = min(ans, result)
                sum -= nums[left]
                left += 1
            }
        }
        return (ans != Int.max) ? ans : 0
    }

 

Complexity analysis

• Time complexity: O(n)
• Space complexity: O(1)

 

 

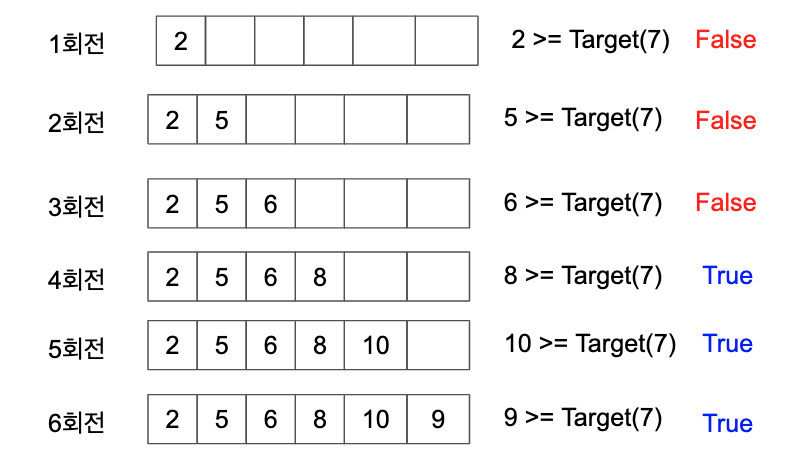
회전이 True 인경우 Result 를 저장합니다. 

Result = i + 1 - left 

 

작은 값의 결과를 저장합니다.

ans = min(ans, result)

 

주어진 배열에서 left 인덱스의 값을 뺍니다.

sum -= nums[left]

 

Left 를 증가시킵니다.

left += 1

 

조건이 만족할때 까지 while sum >= Tartget(7)  위에 과정을 반복합니다.

 

i: 3 ans: 4 = min(ans: 9223372036854775807, result: 4 (i: 3 + 1 - left: 0)  sum: 6 nums[left]: 2
i: 4 ans: 4 = min(ans: 4, result: 4 (i: 4 + 1 - left: 1)  sum: 7 nums[left]: 3
i: 4 ans: 3 = min(ans: 4, result: 3 (i: 4 + 1 - left: 2)  sum: 6 nums[left]: 1
i: 5 ans: 3 = min(ans: 3, result: 3 (i: 5 + 1 - left: 3)  sum: 7 nums[left]: 2
i: 5 ans: 2 = min(ans: 3, result: 2 (i: 5 + 1 - left: 4)  sum: 3 nums[left]: 4

 

마지막 결과는 min(3, 2)  = 2 가 됩니다.

 

마무리

수학적인 지식이 부족하기 때문에 위 과정의 전체를 나열했습니다. 

하지만 점점 발견해 나가는 아신이 되겠습니다.

 

Swift Algorithm Club 에 참여하실 분들은 카카오 오픈 채팅방에 참여해주세요!

https://open.kakao.com/o/gfCPxcJb